今回解説するのは「モンティ・ホール問題」です。
モンティホール問題はかつてアメリカで実際に放送されていたテレビ番組に由来します。
このテレビ番組の司会を務めていたのがモンティ・ホールという人物です。
問題
実際のテレビ番組の流れは次の通りです。

司会者(モンティ):
「ここに3つの扉があります。1つにはあたりを意味する新車が、残りの2つにははずれを意味するヤギが入っています。見事あたりを選ぶことが出来れば新車を景品として差し上げましょう。どの扉を選びますか?」
参加者:
「Aに新車が入ってるはずだ!」
司会者:
「Aですね、わかりました。ではここでBの扉を開けてみましょう。Bの扉の中身はヤギ、はずれの扉でした。今ならまだCの扉に変えてもいいですよ。変えますか?変えませんか?」
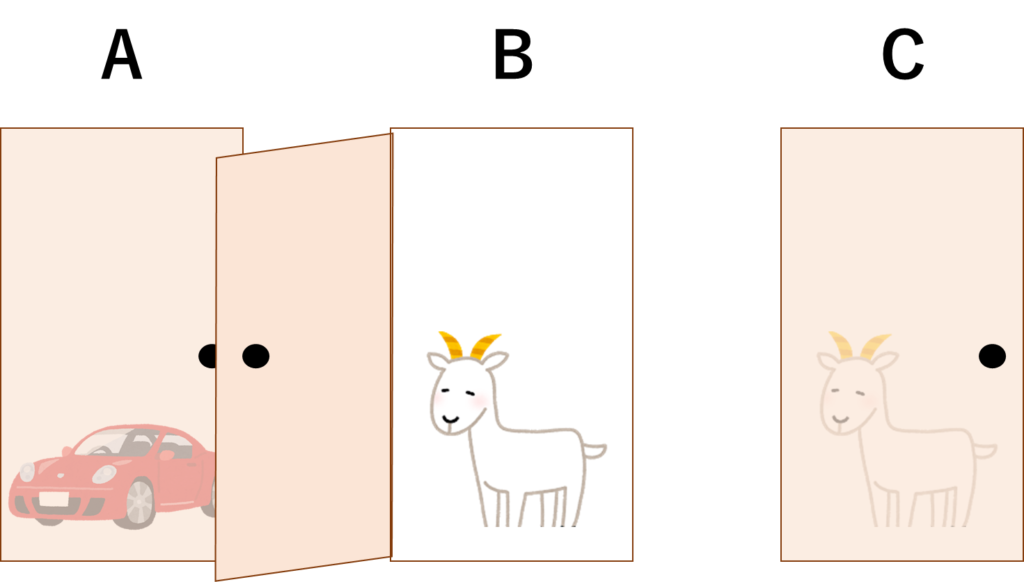
ここで参加者は扉を変えるべきでしょうか?それとも変えないべきでしょうか?
これが「モンティ・ホール問題」です。
司会者がはずれを1つあけています。
直感で考えると残り2つの扉のうちあたりが1つ、はずれが1つだから、どちらも確率は変わらないように思えます。
しかし、これが大きな間違いです!
先に答えを言ってしまうと、変えてあたる確率が2/3、変えないであたる確率が1/3となります。
等しく見えた2つの選択肢のあたる確率は、実際には2倍も違っているのです。
次で詳しく解説します。
解説
前提として注意しなければいけないことがあります。
それは司会者は”必ずはずれの扉を開ける”ということです。
もし司会者がうっかりあたりの扉を開けてしまったら問題として成り立たなくなってしまいます。
実際に起こりうる状況を数え上げてみましょう。
選択肢を変えない時
参加者が
・Aの扉を選ぶ場合
・Bの扉を選ぶ場合
・Cの扉を選ぶ場合
それぞれについて、
(1)Aの扉があたりの時
(2)Bの扉があたりの時
(3)Cの扉があたりの時
を順番に見ていきます。
したがって、選択肢を変えない時は9通りの組み合わせが考えられます。
まずはAの扉を選ぶときです。
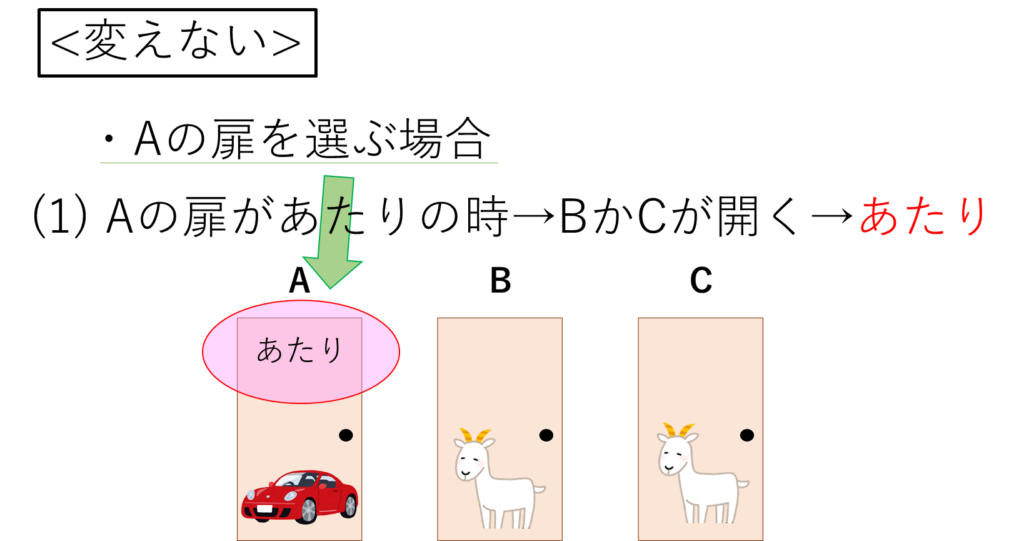
参加者は、最初にAの扉を選びます。
司会ははずれがBとCとわかっているので、どちらかを開けます。
参加者は選択肢を変えないので、そのままAを選びあたります。
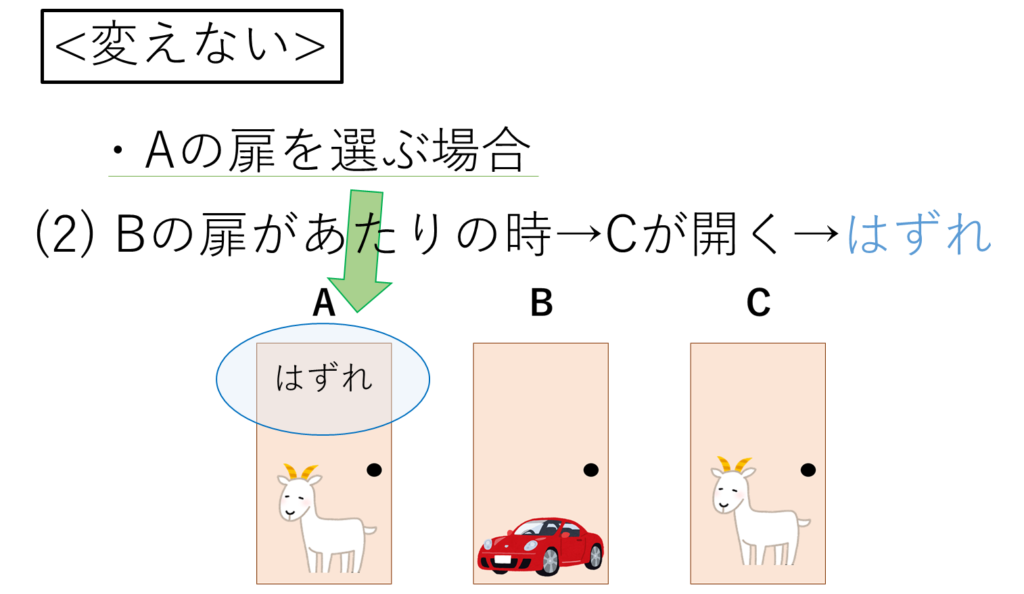
参加者は、最初にAの扉を選びます。
司会者は、はずれであるCの扉を開けます。
参加者は選択肢を変えないので、そのままAを選びはずれます。
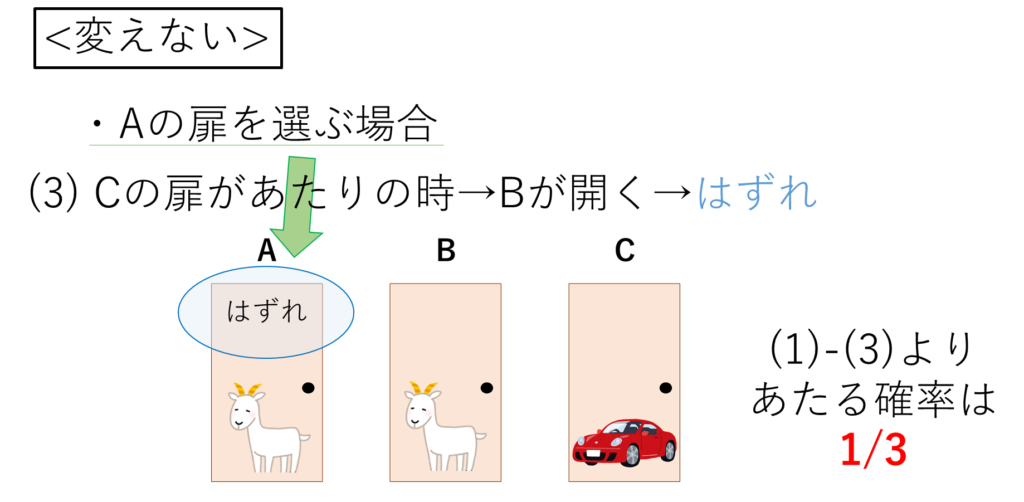
参加者は、最初にAの扉を選びます。
司会者は、はずれであるBの扉を開けます。
参加者は選択肢を変えないので、そのままAを選びはずれます。
以上から、参加者が選択肢を<変えない>状況で、Aの扉を選びあたる確率は1/3となります。
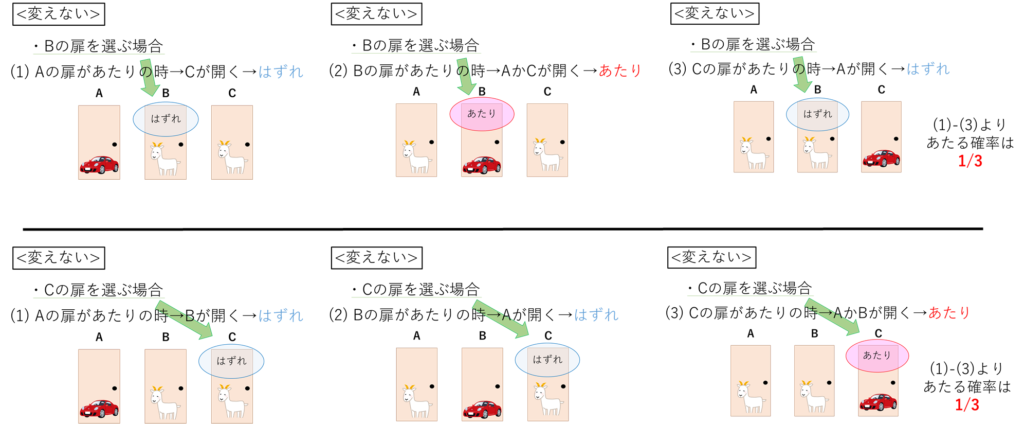
また、参加者が最初にBやCの扉を選ぶときも同じように考えることが出来ます。
以下の写真で確認してください。
結論としては、選択肢を<変えない>状況でのあたる確率は1/3です。
選択肢を変える時
先ほどと同様に、参加者が
・Aの扉を選ぶ場合
・Bの扉を選ぶ場合
・Cの扉を選ぶ場合
それぞれについて、
(1)Aの扉があたりの時
(2)Bの扉があたりの時
(3)Cの扉があたりの時
の9通りの組み合わせを順番に考えていきます。
まず、Aの扉を選ぶ時です。
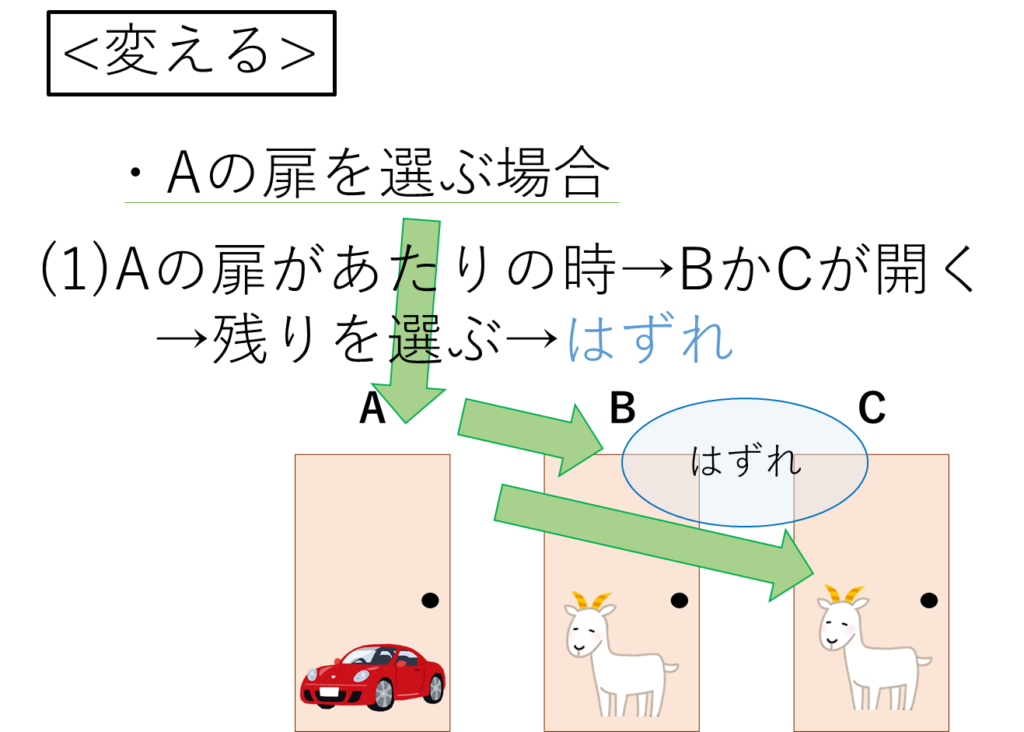
参加者は、最初にAの扉を選びます。
司会ははずれがBとCとわかっているので、どちらかを開けます。
参加者は選択肢を変えるので、開いていないBかCの扉を選びなおし、はずれます。
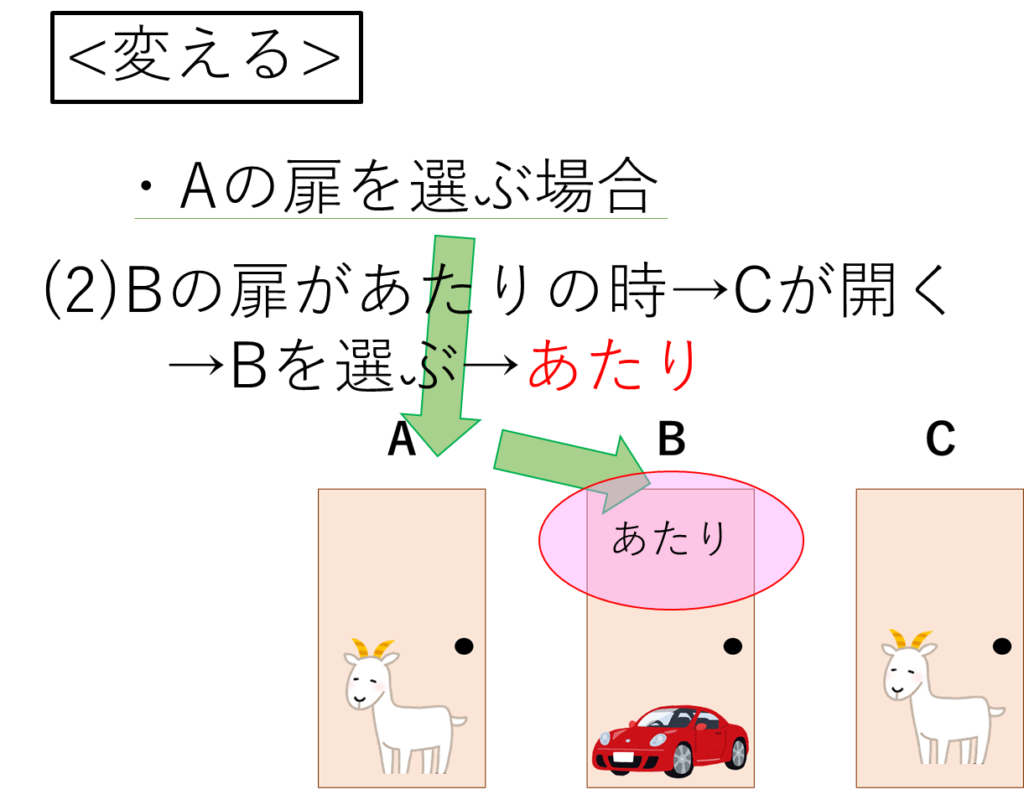
参加者は、最初にAの扉を選びます。
司会は、はずれであるCの扉を開けます。
参加者は選択肢を変えるので、開いていないBの扉を選びなおし、あたります。
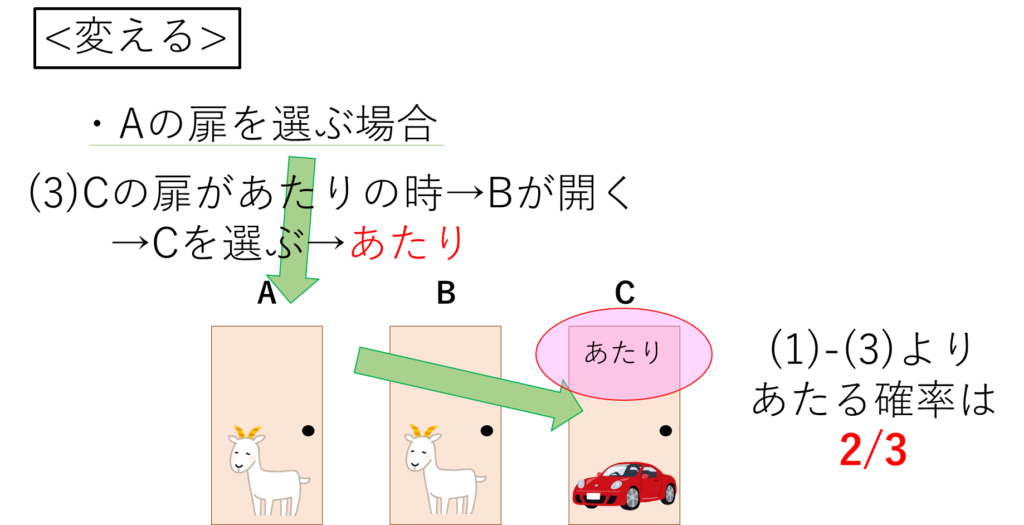
参加者は、最初にAの扉を選びます。
司会は、はずれであるBの扉を開けます。
参加者は選択肢を変えるので、開いていないCの扉を選びなおし、あたります。
以上から、参加者が選択肢を<変える>状況で、Aの扉を選びあたる確率は2/3となります。
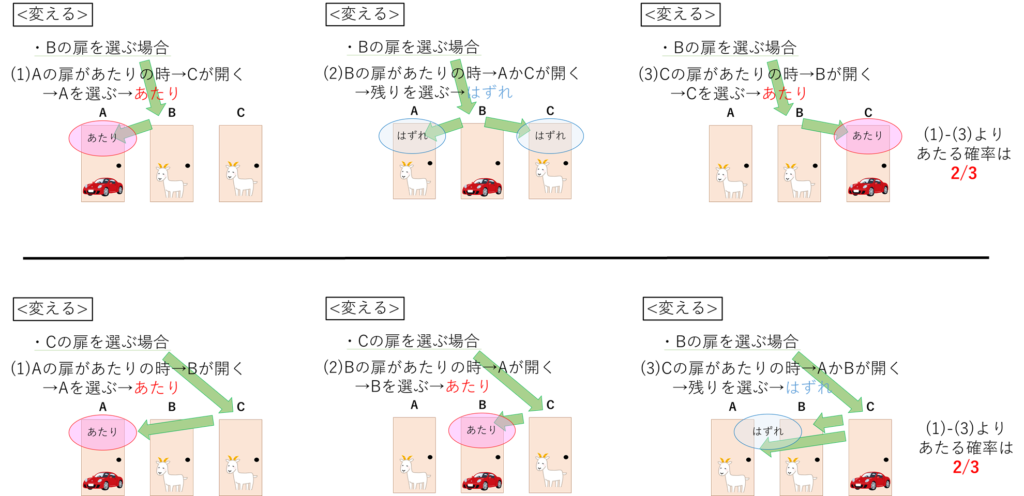
また、参加者が最初にBやCの扉を選ぶときも同じように考えることが出来ます。
以下の写真で確認してください。
結論としては、選択肢を<変える>状況でのあたる確率は2/3です。
検証
ここまで読んで、理論ではわかるけどぱっとしないな…という人が多いと思います。
そこで、実際に検証動画を撮ってみました。
難しく感じた人の理解の助けになるのではないかと思います。
気になる方は以下の動画をぜひご確認ください。
結論
上記で長々と解説しましたが、以下のように簡単に結論を出すことが出来ます。
選択肢を変えない時
最初にあたりを選べばあたる。はずれを選べばはずれる。
→あたる確率は1/3
選択肢を変える時
最初にはずれを選べばあたる。あたりを選べばはずれる。
→あたる確率は2/3
以上が「モンティ・ホール問題」の話でした。
最後までご覧いただきありがとうございました。