今回紹介するのは「白黒ぼうし①」の問題です。
白黒ぼうしに関する問題は色々あるので、1つずつ解説していきます。
問題
2人がある部屋に閉じ込められています。
今からあるゲームをクリアすればこの部屋から出ることが出来ます。
ルール
・2人は白色か黒色のぼうしが被らされて、向き合っています。
・ぼうしの色は2人とも同じかもしれないし、違うかもしれません。
・どちらも相手のぼうしの色は見えますが、自分のぼうしの色は見えません。
・2人同時に自分のぼうしの色を叫び、1人でも当たっていたらクリアです。
このゲームを始める前に2人には5分ほど話し合いの時間が与えられます。
どのように発言すれば、このゲームにクリアできるでしょうか?
解答はこちら↓↓↓
解答
ここから先が解答になります。
「1人は相手のぼうしの色を言い、もう1人は相手のぼうしの色と逆の色を言う」
順番に解説していきます。
解説
登場人物の2人をAとBとします。
AとBのぼうしの色の組み合わせは次のようになります。
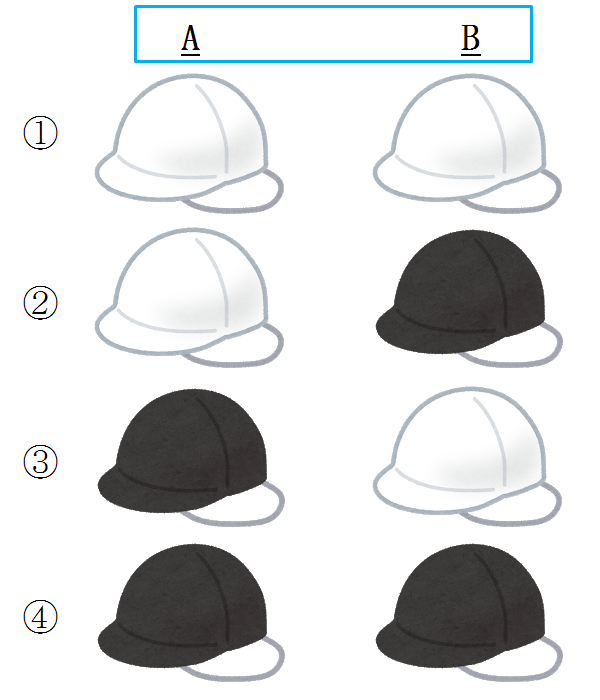
AとBの組み合わせで考えられるのが、
(A,B)=①(白,白)
②(白,黒)
③(黒,白)
④(黒,黒)
の4通りです。
ゲームにクリアする上で大事なのが、2人中1人がぼうしの色を当てることです。
もう1人は外してしまっても問題はありません。
ここで、「AはBのぼうしの色を言い、BはAのぼうしと逆の色を言います」。
こうすることで、上で示した4通りの組み合わせ全てで合格することが出来ます。
以下で確認してでいきます。
・A=白,B=白のとき
上のルールで発言すると、Aは白、Bは黒となります。
Aが自分のぼうしの色を当てることが出来たのでクリアです。
・A=白,B=黒のとき
上のルールで発言すると、Aは黒、Bは黒となります。
Bが自分のぼうしの色を当てることが出来たのでクリアです。
・A=黒,B=白のとき
上のルールで発言すると、Aは白、Bは白となります。
Bが自分のぼうしの色を当てることが出来たのでクリアです。
・A=黒,B=黒のとき
上のルールで発言すると、Aは黒、Bは白となります。
Aが自分のぼうしの色を当てることが出来たのでクリアです。
今回のような問題を考える時は、全てのパターンで成り立つかを考えるのがポイントです。
応用問題
もう一問紹介します。
先程よりは少し難しくなります。
問題
3人の人がある部屋に閉じ込められています。
今からあるゲームをクリアすればこの部屋から出ることが出来ます。
ルール
・3人の人が赤色か青色か黄色のぼうしが被らされて、向き合っています。
・ぼうしの色は3人とも同じかもしれないし、2人だけ同じかもしれないし、3人とも違うかもしれません。
・3人とも残り2人のぼうしの色は見えますが、自分のぼうしの色は見えません。
・3人同時に自分のぼうしの色を叫び、1人でも当たっていたらクリアです。
先程の問題より、人数もぼうしの色も増えました。
このゲームを始める前に3人には5分ほど話し合いの時間が与えられます。
どのように発言すれば、このゲームにクリアできるでしょうか?

解答はこちら↓↓↓
解答
それぞれの色に、赤=0、青=1、黄=2と番号を付けます。
Aは数字の合計が3の倍数になるように色を言い、Bは3で割った余りが1になるように言い、Cは3で割った余りが2になるように言います。
解説
3つの数字の合計を3で割った余りは必ず、0,1,2のどれかになります。
したがって、3人で分担して、0,1,2の全ての組み合わせを言えばクリアできます。
以下で確認してみましょう。
AとBとCの組み合わせで考えられるのが、
(A,B,C)=①(赤,赤,赤)
②(赤,赤,青)
③(赤,赤,黄)
④(赤,青,赤)
⑤(赤,青,青)
⑥(赤,青,黄)
⑦(赤,黄,赤)
⑧(赤,黄,青)
⑨(赤,黄,黄)
⑩(青,赤,赤)
⑪(青,赤,青)
⑫(青,赤,黄)
⑬(青,青,赤)
⑭(青,青,青)
⑮(青,青,黄)
⑯(青,黄,赤)
⑰(青,黄,青)
⑱(青,黄,黄)
⑲(黄,赤,赤)
⑳(黄,赤,青)
㉑(黄,赤,黄)
㉒(黄,青,赤)
㉓(黄,青,青)
㉔(黄,青,黄)
㉕(黄,黄,赤)
㉖(黄,黄,青)
㉗(黄,黄,黄)
の27通りです。
3の3乗ですね。
赤=0、青=1、黄=2とし、これらの組み合わせの合計値を計算すると、
(A,B,C)=①(赤,赤,赤)=0
②(赤,赤,青)=1
③(赤,赤,黄)=2
④(赤,青,赤)=1
⑤(赤,青,青)=2
⑥(赤,青,黄)=3
⑦(赤,黄,赤)=2
⑧(赤,黄,青)=3
⑨(赤,黄,黄)=4
⑩(青,赤,赤)=1
⑪(青,赤,青)=2
⑫(青,赤,黄)=3
⑬(青,青,赤)=2
⑭(青,青,青)=3
⑮(青,青,黄)=4
⑯(青,黄,赤)=3
⑰(青,黄,青)=4
⑱(青,黄,黄)=5
⑲(黄,赤,赤)=2
⑳(黄,赤,青)=3
㉑(黄,赤,黄)=4
㉒(黄,青,赤)=3
㉓(黄,青,青)=4
㉔(黄,青,黄)=5
㉕(黄,黄,赤)=4
㉖(黄,黄,青)=5
㉗(黄,黄,黄)=6
となり、0~6までの数字に分類されます。
0~6までの数字を3で割った余りは必ず、0,1,2のどれかになります。
したがって、3人で分担して0,1,2の全ての組み合わせを言えばクリアできます。
今回はここまでです。
最後までご覧頂きありがとうございました。