今回は「病気の誤検査」について解説します。
メディアなどが報道する数字のトリックに惑わされないように気を付けましょう。
問題
【設定】
日本国内でコロンウイルスという病気が広がりつつあります。
今はまだ感染者は少なく、日本の人口の1/100が感染している程度です。
つまり日本の人口を1億人とすると、国内だけで100万人がコロンウイルスに感染していると考えられます。
このコロンウイルスに感染しているかどうかはPCL検査を受けることで陰性/陽性が判定されます。
しかしこのPCL検査の結果は絶対ではなく、以下の特徴があります。
1. 実際にコロンウイルスに感染している人にPCL検査をすると、100%の確率で陽性と判定される。
2. 実際にはコロンウイルスに感染していない人にPCL検査をすると、90%の確率で陰性と判定される。
【問題】
ある時あなたはPCL検査を受けて陽性と判断されました。
あなたが”実際に”コロンウイルスに感染している確率は何%でしょうか?
解説
先に結論を言います。
”実際に”コロンウイルスに感染している確率は、たったの9.2%です。
直感的には確率はもっと高いと思ったのではないでしょうか?
それはPCL検査の結果が多くの場合に正確であるからです。
ではなぜ、確率はこんなにも小さくなるのでしょうか。
実際に1万人に対して検査をしてみる場合を考えればわかりやすいです。
10,000人に対してPCL検査を行うと
下図のように、10,000人に対してPCL検査を行う場合を考えます。
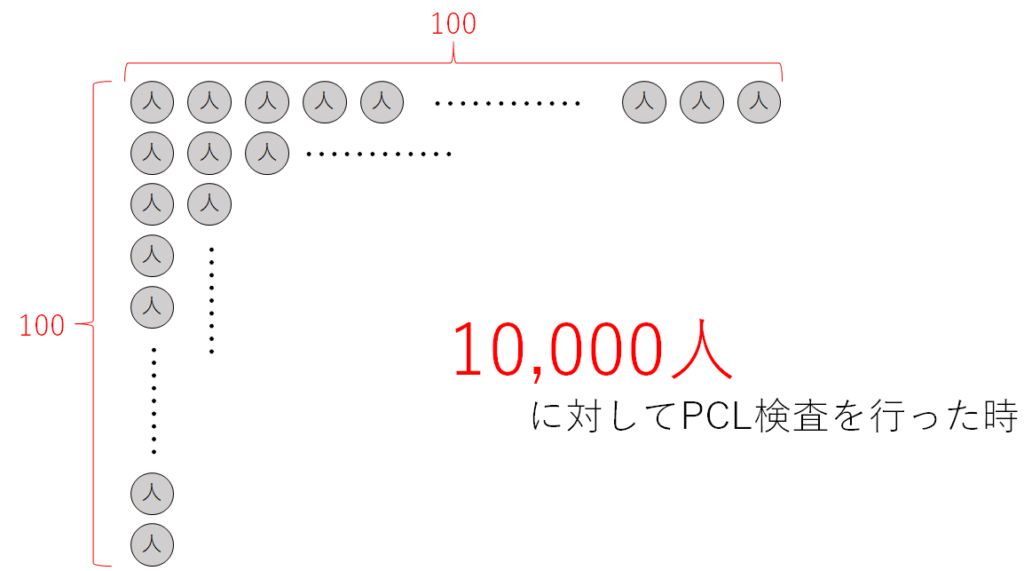
まずは、この10,000人のうち、”実際に”コロンウイルスに感染している人数を数えます。
設定として人口の1/100が感染しているので、10,000人のうち100人がコロンウイルスに感染しています。
一方で、9,900人は感染していません。
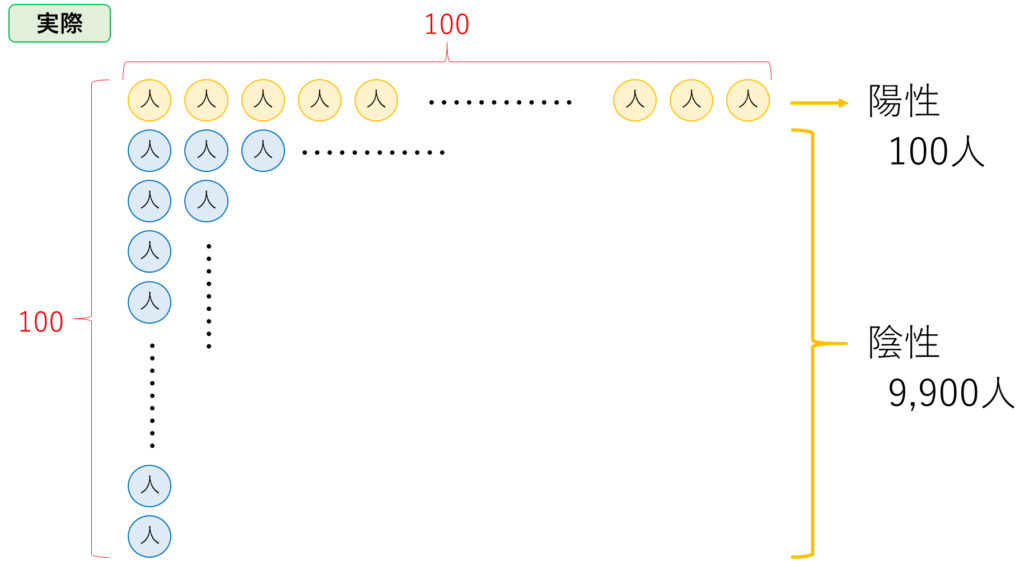
この場合で、PCL検査を行った時の”検査結果”について考えます。
PCL検査の特徴で、感染していない人に対しては10%の確率で陽性と判定します。
したがって、感染していない9,900人のうち、990人は陽性と判定されてしまいます。
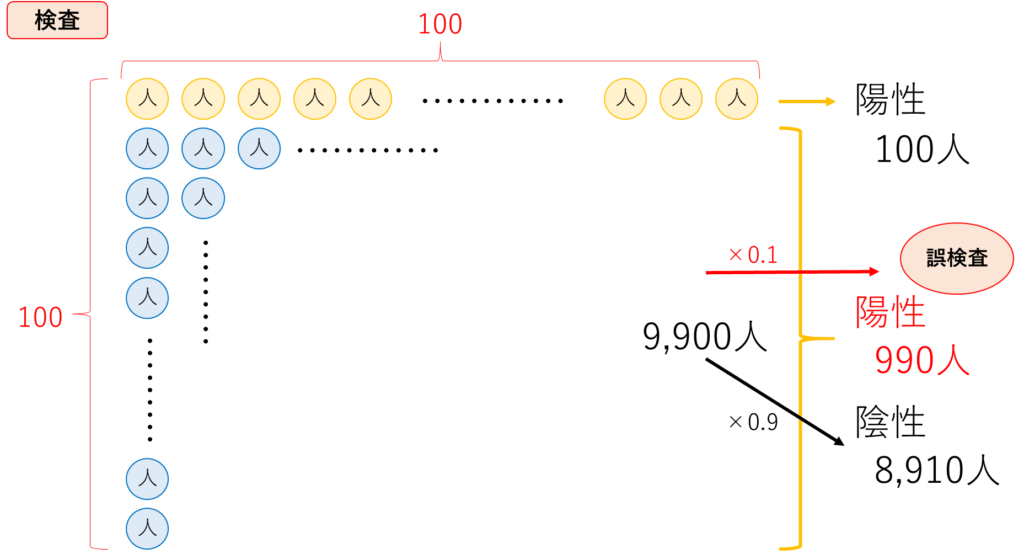
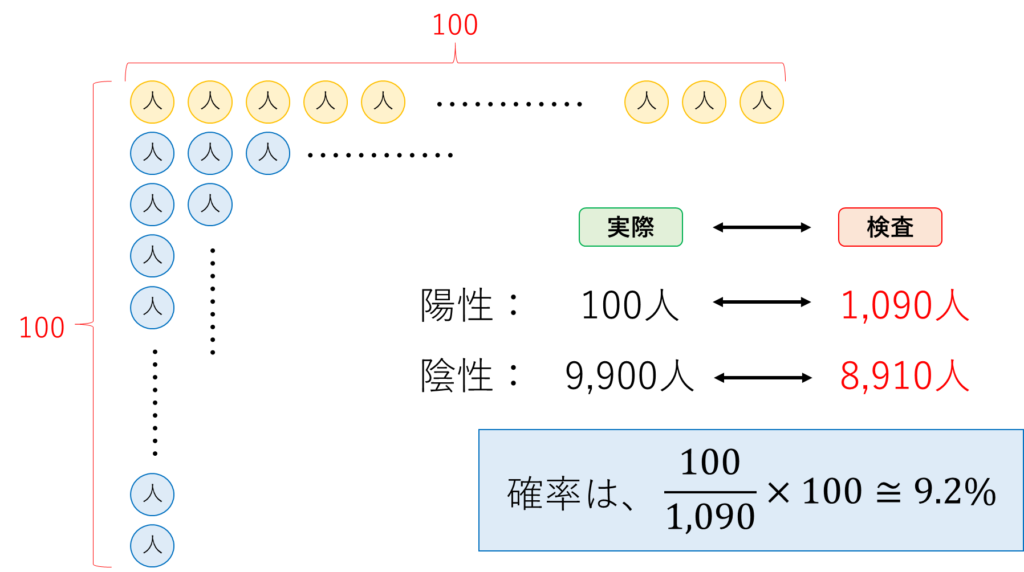
以上から、今回の問題である確率を考えると次のようになります。
PCL検査で陽性と判定される人数は、1,090人。
このうち”実際に”感染しているのは100人だけです。
したがって、求める確率は、100/1,090×100で約9.2%となります。
最後に、なぜ検査が正確であるように感じるのに、確率がここまで低くなるのかについて説明します。
私たちは、PCL検査が比較的正確であるということに注目してしまいますが、そもそもコロンウイルスの感染者数自体が少ないことを見落としています。
検査のエラー率は10%で、これはコロンウイルスの感染割合1%よりも高いです。
このような状況では、陽性と判断されたとき、実際に陽性であるよりも誤検査であるほうが多くなります。
今回の問題は条件付確率で考えることが出来ます。
以下の図を参考にしてください。

おまけ
もう1問だけ似たような問題を紹介しておきます。
【問題】
クラゲという生き物は体の99%が水分です。
100gの重さのクラゲが浜辺に打ち上げられています。
太陽の日差しにより、水分量が98%になるまで体内の水分が蒸発してしまいました。
このクラゲの重さは何gになったでしょうか?
【解答】
100gの時のクラゲの成分は次の通りです。
水分:99g
有機物:1g
水分量=99/(99+1)=99%
クラゲの有機物量は変化しないことを念頭に置いて、98%の時の成分を考えます。
水分:Xg
有機物:1g
水分量=X/(X+1)=98%
上記のXを求めると、X=49gとなります。
したがって、クラゲの重さは50gまで減ってしまいました。
今回はここまでです。お疲れさまでした。