今回紹介するのは「20枚のコイン」の問題です。
問題
真っ暗な部屋の中にあなたが閉じ込められており、部屋の中にはコインが20枚置いてあります。
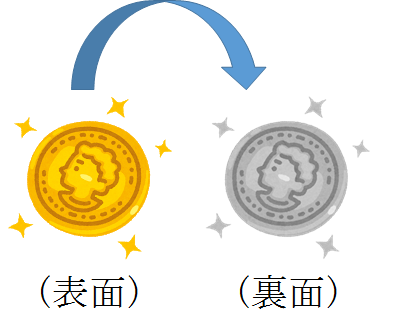
コインの表面は金貨、裏面は銀貨となっており、20枚中表面で置いてあるのは12枚、裏面は8枚です。
この20枚を2つのグループに分けたとき、裏面で置いてあるコインの枚数が同じになるように操作をすればあなたはこの部屋から脱出できます。
どのように操作をすればいいでしょうか?
<条件>
・表裏があるコインが20枚あり、表が12枚、裏が8枚で置いてある。
・見ても触ってもコインの裏表は区別できない。
・出来る操作は、①コインを2つのグループに分ける、②好きなコインをひっくり返す。
・2グループで、裏となっているコインの枚数を同じにするにはどうすればいいか?
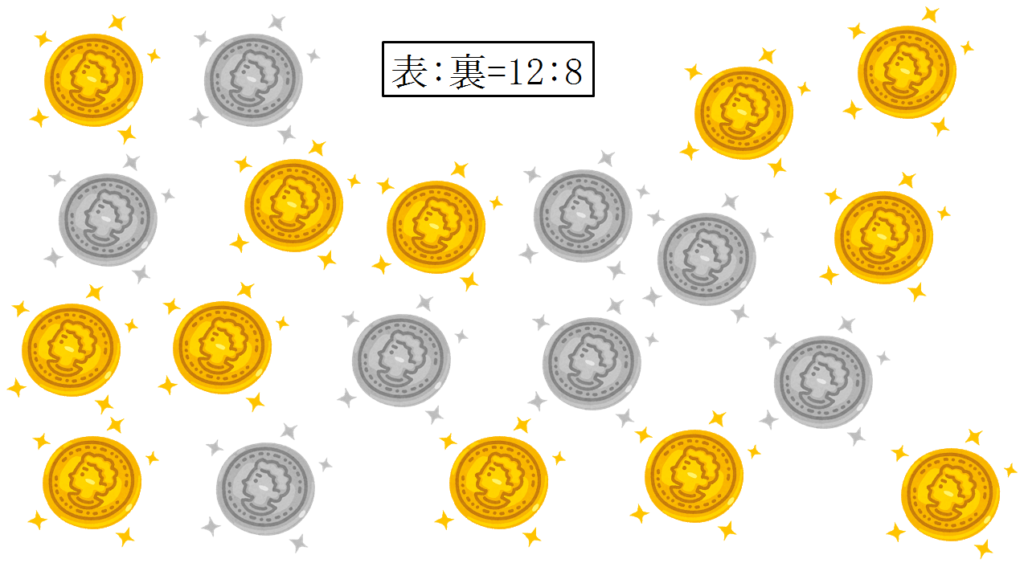
解答はこちら↓↓↓
解答
8枚(裏面の枚数)を取り出し、その全てをひっくり返す。
そうすることで、12枚グループと8枚グループの裏面の枚数は等しくなります。
以下で取り出した8枚の種類に関して、順番に確認してみましょう。
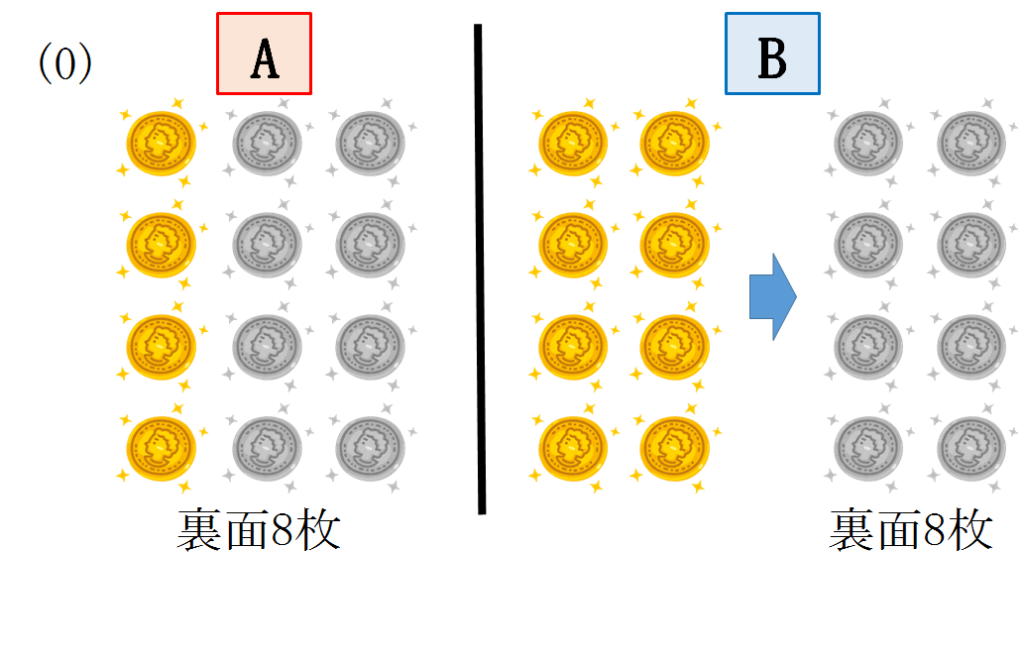
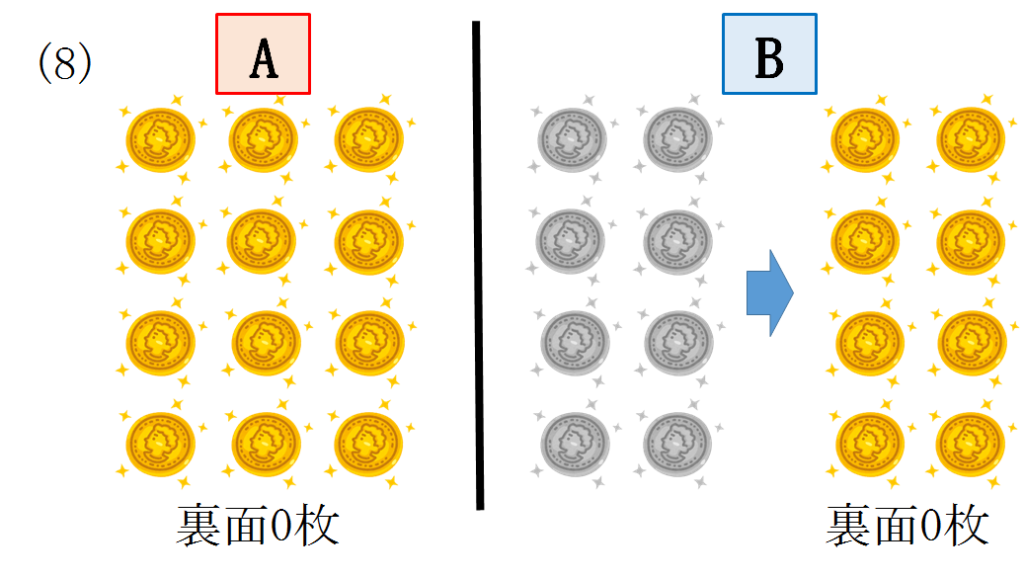
(0)取り出した8枚のうち裏面が0枚のとき
12枚グループをA、8枚グループをBとします。
Bの8枚はすべて表面なので全てをひっくり返すとBは裏面が8枚になります。
したがってA,Bともに裏面の枚数は8枚になります。
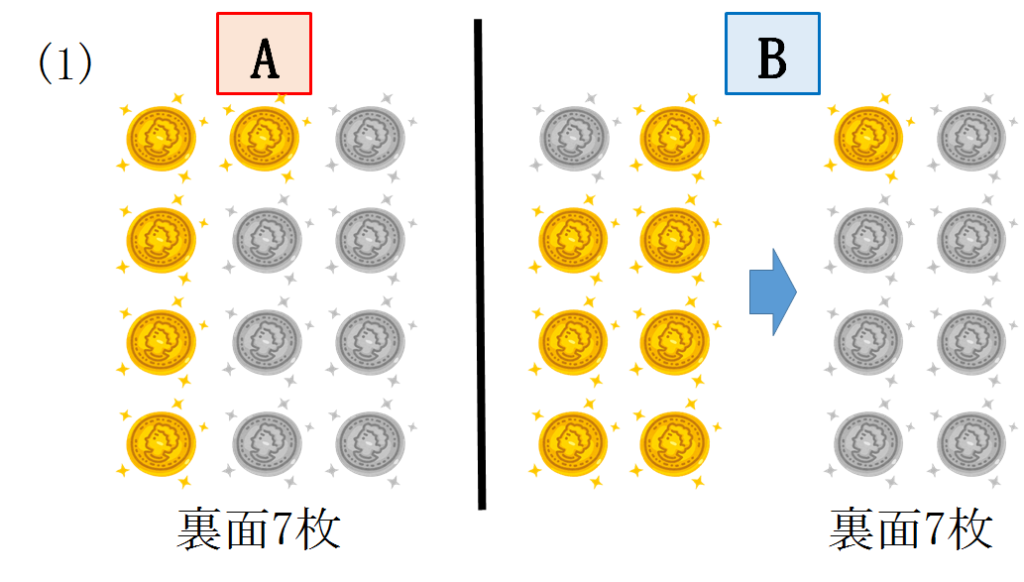
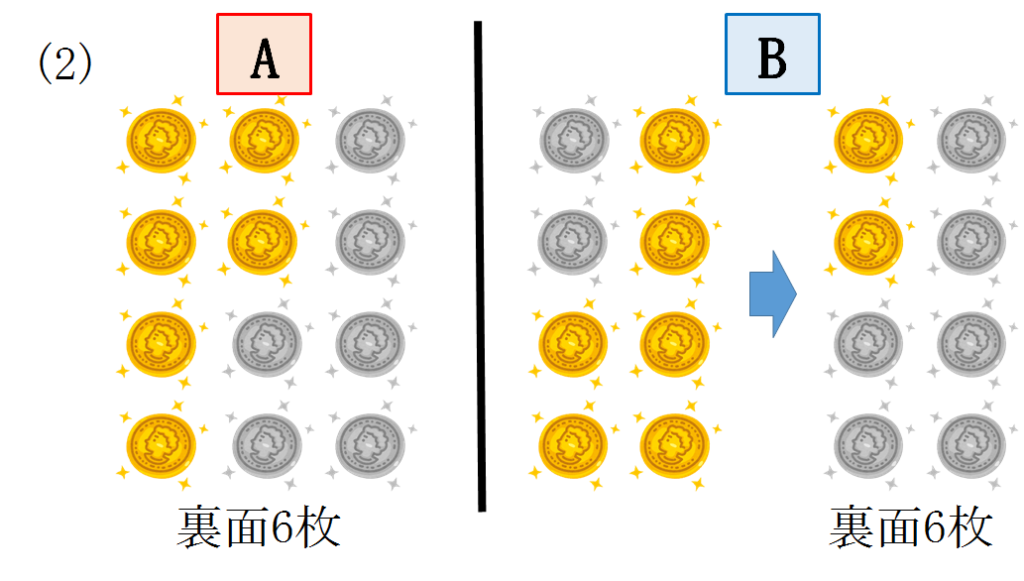
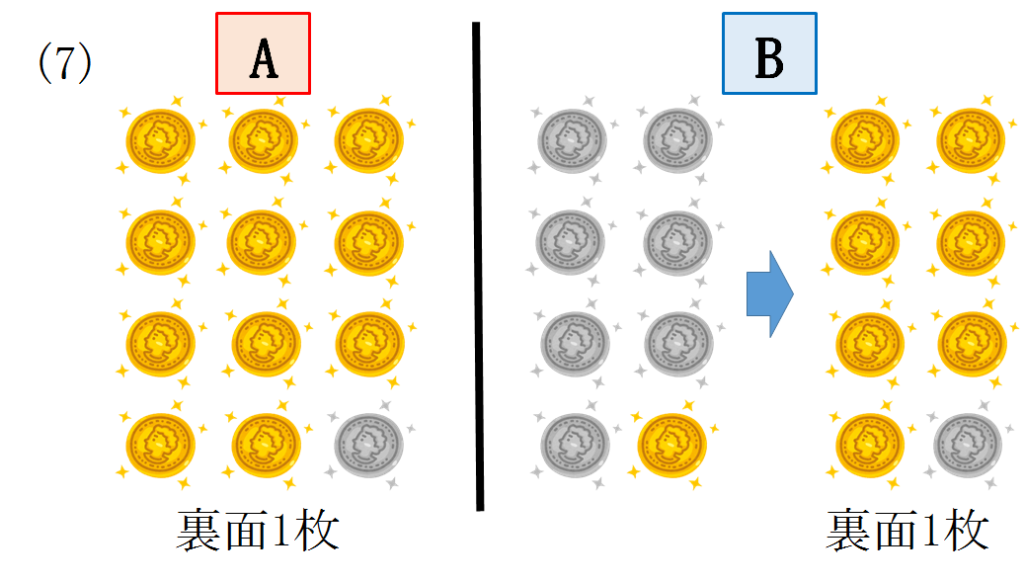
(1)取り出した8枚のうち裏面が1枚のとき
Bは7枚が表面なので全てをひっくり返すとBは裏面が7枚になります。
したがってA,Bともに裏面の枚数は7枚になります。
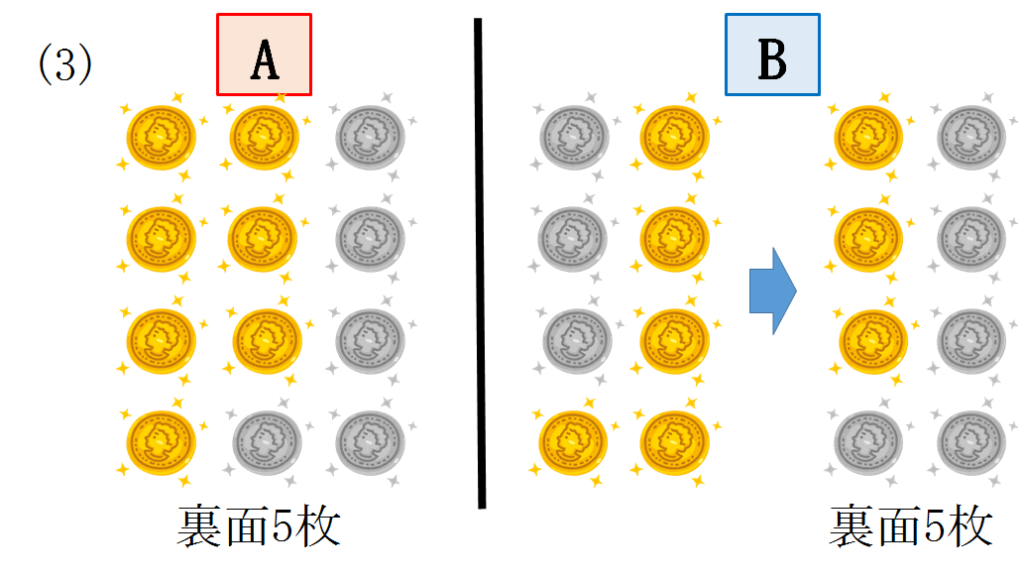
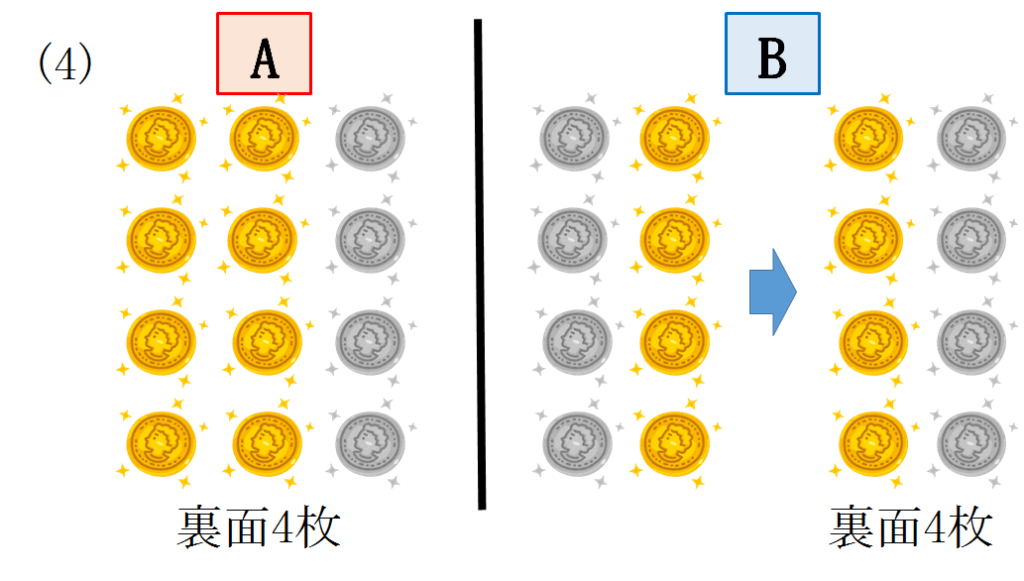
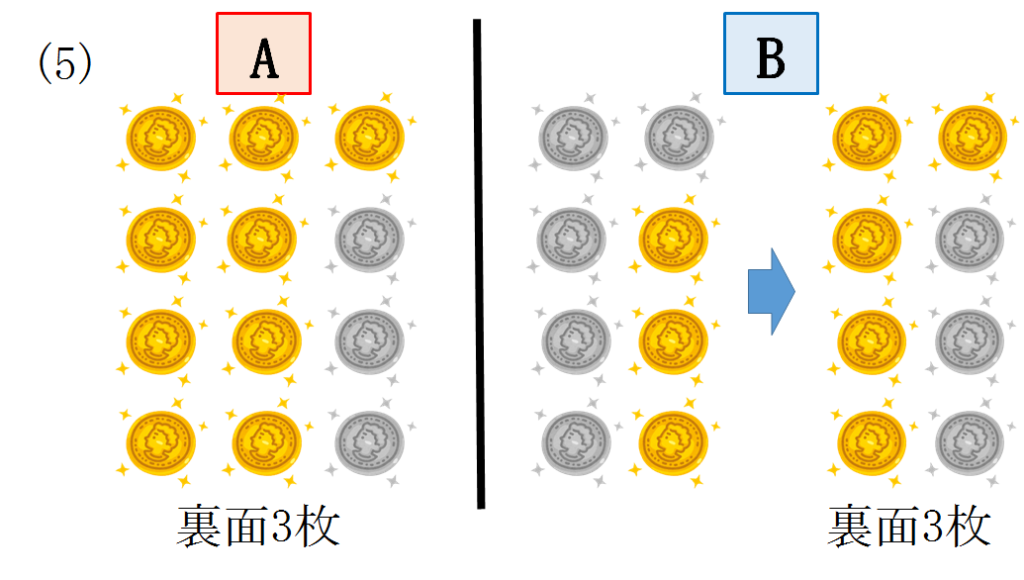
以下同様に考えることが出来ます。
文章での解説は画像で確認してください。
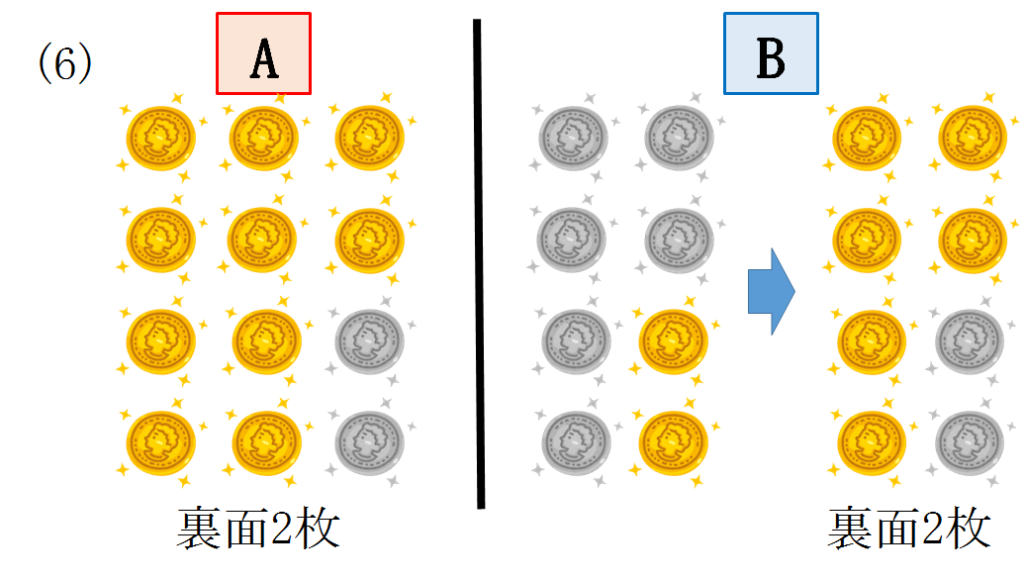
より具体的な解説
今回の問題を考える上で重要な要素は、「余事象」です。
高校数学で確率を学んでいる方は、余事象という言葉を聞いたことがあると思います。
考え方
8枚を取り出したとき、Bグループに含まれている裏面の枚数をn枚とします。
一番最初、20枚のうち裏面は8枚なので、Aグループに残っている裏面の枚数は8-n枚になります。
ここで、Bグループの表面は8-n枚です。
Bグループのコインを全てひっくり返すことで、表面と裏面が入れ替わり、裏面の枚数が8-n枚になります。
以上の考え方で、AグループとBグループの裏面の枚数が必ず等しくなることがわかります。
今回の「20枚のコイン」の問題は以上です。
次回のパズルもぜひ御覧ください。